运筹学作业代写
运筹学 Operations research 作业代写,excellentdue为您提供数学大类作业、考试代写包含运筹学网课,exam代考,assignment代写,作业辅导等,如果您需要运筹学相关学术支持服务请联系我们的客服哦
什么是运筹学
运筹学是近代应用数学的一个分支,主要是研究如何将生产、管理等事件中出现的运筹问题加以提炼,然后利用数学方法进行解决的学科。运筹学是应用数学和形式科学的跨领域研究,利用像是统计学、数学模型和算法等方法,去寻找复杂问题中的最佳或近似最佳的解答。运筹学经常用于解决现实生活中的复杂问题,特别是改善或优化现有系统的效率。
运筹学的思想在古代就已经产生了。但是作为一门数学学科,用纯数学的方法来解决最优方法的选择安排,却是在二十世纪四十年代才开始兴起的一门分支。
运筹学主要研究经济活动和军事活动中能用数量来表达的有关策划、管理方面的问题。当然,随着客观实际的发展,运筹学的许多内容已经深入到日常生活当中去了。
随着科学技术和生产的发展,运筹学已渗入很多领域里,发挥了越来越重要的作用。运筹学本身也在不断发展,现在已经是包括好几个分支的数学部门了。
运筹学在英国称为operational research,在美国称为operations research,英文缩写是OR。中国科学工作者取“运筹”一词作为OR的意译,包含运用筹划、以策略取胜等意义。
运筹学发展简史
Operational research(运筹学)一词最早出现于1938年。当时英国波德塞雷达站负责人A.P.罗提出对整个防空作战系统的运行研究,以解决雷达站合理配置和整个空军作战系统协调配合来有效地防御德机入侵的问题。1940年9月英国成立了由物理学家P.M.S.布莱克特领导的第一个运筹学小组。后来发展到每一个英军指挥部都成立运筹学小组。1942年美国和加拿大都相继建立了运筹学小组。这些运筹学小组在确定护航舰队的规模、开展反潜艇战的侦察、组织有效的对敌轰炸等方面作了大量研究,为运筹学有关分支的建立作出了贡献。
第二次世界大战后,在这些军事运筹学小组中工作过的科学家转向研究在民用部门应用运筹学方法的可能性,从而促进了在民用部门应用运筹学的发展。1947年G.B.丹齐克在研究美国空军资源配置问题时提出线性规划及其通用解法──单纯形法。50年代初用电子计算机求解线性规划问题获得成功。1951年P.M.莫尔斯和G.E.金布尔合著《运筹学方法》一书正式出版,标志着运筹学这一学科已基本形成。到50年代末,美国大企业在经营管理中大量应用运筹学。开始时主要用于制订生产计划,后来在物资储备、资源分配、设备更新、任务分派等方面应用和发展了许多新的方法和模型。60年代中期,运筹学开始用于服务性行业和公用事业。一些发达国家的企业、政府、军事等部门都拥有相当规模的运筹学研究机构,专门从事有关方法和建模的研究,为决策提供科学的依据。英国在1948年成立了运筹学俱乐部,1954年改名为英国运筹学会,出版《运筹学季刊》。美国在1952年成立了美国运筹学会,出版《运筹学》杂志。1957年在英国牛津大学召开第一届国际运筹学会议,以后每隔3年举行一次。1959年成立国际运筹学联合会(IFORS)。
中国在1956年曾用过“运用学”的名字,于1957年正式定名为“运筹学”,于1980年成立中国运筹学会(ORSC),并于1982年加入国际运筹学联合会(IFORS)。
运筹学学科内容
运筹学研究的内容十分广泛,其主要分支有:线性规划、非线性规划、整数规划、几何规划、大型规划、动态规划、图论、网络理论、博弈论、决策论、排队论、存贮论、搜索论等。
应用运筹学处理问题时分为5个阶段。
①规定目标和明确问题:包括把整个问题分解成若干子问题,确定问题的尺度、有效性度量、可控变量和不可控变量,以及用来表示变量界限和变量间关系的常数和参数。
②收集数据和建立模型:包括定义关系、经验关系和规范关系。
③求解模型和优化方案:包括确定求解模型的数学方法,程序设计和调试,仿真运行和方案选优。
④检验模型和评价解答:包括检验模型的一致性、灵敏度、似然性和工作能力,并用试验数据来评价模型的解。一致性是指主要参数变动时(尤其是变到极值时)模型得出的结果是否合理;灵敏度是指输入发生微小变化时输出变化的相对大小是否合适;似然性是指对于真实数据的案例,模型是否适应;工作能力则是指模型是否容易解出,即在规定时间内算出所需的结果。
⑤方案实施和不断优化:包括应用所得的解解决实际问题,并在方案实施过程中发现新的问题和不断进行优化。上述5个阶段往往需要交叉进行,不断反复。
现代运筹学方法强调黑箱方法、数学模型和仿真运行。它重视系统的输入输出关系,即问题所处的环境条件和问题中主要因素与环境间的关系,而不追求系统内部机理,因而易于达到从系统整体出发来研究问题的目的。常用的数学模型有:分配模型、运输模型、选址模型、网络模型、计划排序模型、存储模型、排队模型、概率决策模型、马尔可夫模型等。模型求解往往成为应用计算机程序进行仿真运行。现在已有各种运筹学软件包供应,使运筹学可以处理相当复杂的大型问题。随着运筹学应用于社会大系统,仅靠定量分析已难以找到合理的优化方案,人们常采用定量与定性相结合、在定量分析的基础上进行定性分析的方法。因此,在许多情况下已很难划分运筹学、系统分析与政策分析的界限。
运筹学展望
运筹学正朝着3个领域发展:运筹学应用、运筹科学和运筹数学。
现代运筹学面临的新对象是经济、技术、社会、生态和政治等因素交叉在一起的复杂系统,因此必须注意大系统、注意与系统分析相结合,与未来学相结合,引入一些非数学的方法和理论,采用软系统的思考方法。总之,运筹学还在不断发展中,新的思想、观点和方法不断出现。
运筹学分支
- 数学规划
- 线性规划
- 非线性规划
- 整数规划
- 目标规划
- 动态规划
- 参数规划
- 随机规划
- 组合最优化
- 图论
- 排队论
- 存贮论
- 对策论(博弈论)
- 决策论
- 搜索论
- 统筹论
- 最优化
- 启发式演算法
- 计算机仿真
- 数据挖掘
- 预测学
- 软系统方法
- 认知映射
运筹学在经济管理中的应用实例
运筹学作为一门新兴科学,其应用范围是十分广泛的。对于不同类型问题,运筹学都有着不同的解决方法,因而形成了许多分支学科。它们虽然各有特性,但在运用系统观念分析问题,并对问题建立模型求解这两点上都是共同的。这些分支学科包括线性规划、非线性规划、动态规划、决策分析等等,在此主要介绍线性规划和动态规划在经济管理中的一些应用。
1.线性规划。
线性规划是目前在经济管理中应用最广泛的一种优化法,它的理论已经十分成熟,可以应用于生产计划、物资调用、资源优化配置等问题。它主要研究的是经济管理活动中经常遇到的两类问题:一类是在有限的劳动力、设备、资金等资源条件下,研究如何合理安排,取得最大的经济效果(如生产经营利润);另一类是为了达到一定的目标(生产指标或其它指标),研究如何组织生产,或合理安排工艺流程,或调整产品的成份等等,以使消耗资料(人力、设备台数、资金原材料等)为最少去实现目标。这类统筹规划的问题用数学语言表达(即数学模型),先根据问题要达到的目标选取适当的变量,问题的目标通过用变量的函数形式表示(称为目标函数),对问题的限制条件用有关变量的等式或不等式表达(称为约束条件)。当变量连续取值,且目标函数和约束条件均为线性时,称这类模型为线性规划的数学模型。下面举例说明线性规划在经济管理中的应用。
【例1】生产计划问题(资源配置)。某制药厂生产甲、乙两种药品,生产这两种药品要消耗某种维生素。生产每吨药品所需要的维生素量及所占设备时间见表1。该厂每周所能得到的维生素量为160kg、每周设备最多能开15个台班。且根据市场需求,甲种产品每周产量不应超过4t。已知该厂生产每吨甲、乙两种产品的利润分别为5万元及2万元。问该厂应如何安排两种产品的产量才能使每周获得的利润最大?
| 每吨产品的消耗 | 每周资源总量 | ||
| 甲 | 乙 | ||
| 维生素/kg | 30 | 20 | 160 |
| 设备/台班 | 5 | 1 | 15 |
解:设该厂每周安排生产甲种药品的产量为x1(t),乙种产量为x2(t),则每周所能获得的利润总额为Z = 5x1 + 2x2数学模型为 maxZ = 5x1 + 2x2(目标函数)
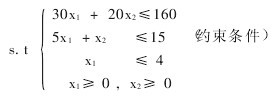
用图解法或单纯型方法解略,本题的最优解X * = (2,5),最优值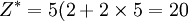 即该厂每周安排生产甲种药品生产量为2t,乙种产量为5t,每周可获得最大利润为20万元。
即该厂每周安排生产甲种药品生产量为2t,乙种产量为5t,每周可获得最大利润为20万元。
2.动态规划。
动态规划是运筹学的一个分支,是一种解决多阶段决策过程最优化的数学方法,它把困难的多阶段的决策问题分解成一系列相互联系的较容易解决的单阶段决策问题,通过解决这一系列单阶段决策问题来解决多阶段决策问题。以寻求最优决策序列的方法,动态规划研究多阶段决策过程的总体优化,即从系统总体出发,要求各阶段决策所构成的决策序列使目标函数值达到最优。在经济管理方面,动态规划可以用来解决最优路径问题、资源分配问题、生产调度问题、库存问题、装载问题、排序问题、设备更新问题、生产过程最优控制问题等等、所以它是现代经济管理中的一种重要的决策方法。
动态规划是求解某类问题的一种方法,是考察问题的一种途径,而不是一种特殊算法(如线性规划方法是一种算法),现举例说明动态规划在经济管理中的应用。
【例2】库存-销售问题。某公司计划在1月至4月份从事某种商品的经营。已知它的仓库最多可存储1000件这种商品,该公司开业时有存货500件,并根据预测知道,该种商品1月至4月的进价和售价如表2所示。问如何安排进货量和销售量,使该公司获得最大利润?(假设四月底库存为零。)
解:若将1月至4月份的购销安排作为阶段k(k=1,2,3,4),那么该问题就是一个四阶段决策问题。
| 月份(k) | 1 | 2 | 3 | 4 |
| 进价Ck(百元/件) | 10 | 9 | 11 | 15 |
| 售价Pk(百元/件) | 12 | 9 | 13 | 17 |
选择第k月初公司的存货量作为状态变量S_k,第k月的销售量和进货量分别作为决策变量U_k和V_k。
状态转移方程是
Sk = Sk + Vk − Uk k=1,2,3,4
而
 k=1,2,3,4
k=1,2,3,4
由已知,S1 = 500;假想有第五价段,S5 = 0。
阶段收益函数为rk(Sk;Uk,Vk) = PkUk − CkVk
动态规划基本方程为
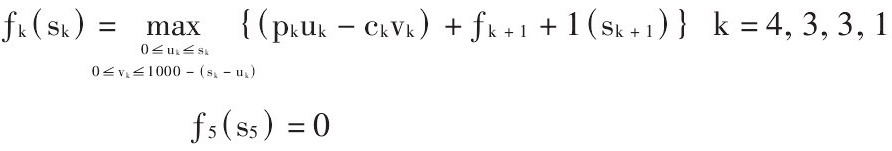
采用逆序法递推计算(略)
最后得到该问题的最优策略见表3
| 月份 | 月初存货量S_k(件) | 销售量U_k(件) | 进货量V_k(件) |
| 1 | 500 | 500 | 0 |
| 2 | 0 | 0 | 1000 |
| 3 | 1000 | 1000 | 1000 |
| 4 | 1000 | 1000 | 0 |
则该公司获得的最大利润为f1(s1) = f1(500) = 16000(百元)=160(万元)


